Interest Rate

What’s an Interest Rate?

An interest rate is the amount a borrower pays a lender to use the lender’s capital. It is typically given as an annual value or annual percentage rate (APR). The actual amount the borrower pays is determined by the amount of the loan, which is called the principal.

A lender usually charges a higher rate for a riskier loan. This is determined by the borrower’s credit, the period of time the borrower will be using the capital and the market alternatives available to both parties.

Calculating an Interest Rate Payment

The equation for calculating an annual interest rate payment is:

• Payment = Principal x Annual Interest Rate

For a monthly payment:

• Payment = Principal x Annual Interest Rate / 12 months

Fixed Rates vs. Floating Rates

A fixed interest rate remains unchanged for the period of the loan. For example, company XYZ asks bank A to borrow $100,000 for new equipment. Company XYZ believes the new equipment will generate enough money to repay the entire loan in 5 years.

Bank A is willing to lend XYZ the money if XYZ pays it a fixed 5% annual interest rate and return of the $100,000 at the end of 5 years. Also, bank A would like XYZ to make monthly payments and it cannot return the money earlier than five years. Under this agreement, XYZ will make 60 interest payments of $416= $100,000x0.05/12 and then return the original $100,000 to A.

A floating interest rate can change as a function of a base rate that banks charge one another, e.g., LIBOR. In the example above, company XYZ may not want to make a commitment to a five year, fixed-rate loan.

Another option then would be a short term loan or a line of credit with a rate that floats and the option to repay the principal at any time. In this case, on day one, the company borrows $100,000 at a rate of LIBOR (1%) + 1%, resulting in a monthly interest payment of $166 (calculation: $100,000x0.02/12).

After one year, LIBOR rises to 5%, which raises the interest payment to $500 (calculation: $100,000x0.06/12). However, the equipment XYZ bought generated the $100,000 to pay off the original loan earlier than anticipated, so the company returns $100,000 to A after the first year, ending its payment obligations.

Compound Interest

Compound interest is used when the payments of a loan or investment are added to the original principal instead of being paid out. The borrower avoids regular payments but will pay more interest when it’s time to pay off the loan. The lender or investor gives up the cash flow from regular payments, but earnings are amplified due to the increasing principal.

The formula for interest compounded yearly is:

• Total Amount= Principal x((1+Annual Interest Rate)^periods)

If the loan is compounded monthly the formula is:

• Total Amount = Principal x (1+((Annual Interest Rate/12)^months))

The equation for each payment, which is plowed back into the principal is:

• Total Amount = Principal x ((1+((Annual Interest Rate/12)^months))-1)

For instance, if bank A and company XYZ agreed to a loan of $100,000 for 2 years, compounded monthly, with only one payment required at the end of the loan, the result would be $110,494 (calculation: ($100,000x(1+((.05/12)^24).

Compare this to simple interest on $100,000 at a fixed 5% rate paid off in 2 years, which is $110,000 (calculation: (($100,000x.05)x2)+100,000). That’s a difference of $494 in bank A’s favor.

Compound interest is used to account for inflation. For example, If inflation is 3% per year, the equivalent buying power 24 years ago of $100,000, compounded annually, would now be $203,279.41 (calculation: $100,000x(1.03^24)).

Finding Interest Rate Information At Investing.com

The World Government Bonds page at Investing.com provides all the interest rates available for investing in sovereign debt instruments around the world. Filters at the top of the page allow users to drill down to specific markets by continent, country, and maturity.

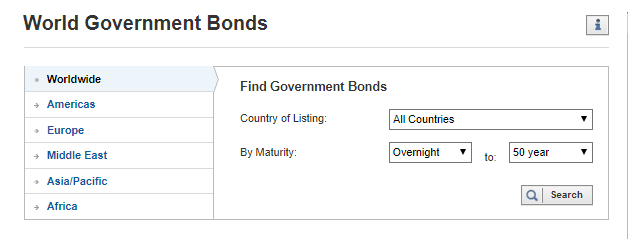
Each instrument in the tables has its own page with detailed information about that market, e.g. US 10-year Treasury.