Little-SIS Issues First Warning In Three Months

Last fall I spoke at an active money management conference, where I introduced about a half-a-dozen or more weekly inter-market ETF models designed to measure “risk acceptance” in equities. The subject of this post features one of the more basic models, which was partially inspired by the highly recommended “The Lawyer Trader” blog.
 
This particular model is named “Sensitive Issues Scoring,” or here “Little-SIS” for short (she has a big sister, after all). The idea is to construct an aggregate oscillator using various ETFs that are especially sensitive to the economy, and may therefore either lead or emphasize broader market trends. When I use the phrase, “emphasize”, I mean exaggerate in such a way that makes the signal wholly unambiguous and cross-confirmed.
 
Assessing Risk Acceptance
 
In fact, the model below uses nine diverse, economically sensitive ETFs to “paint the tape” in the top pane with three risk states, here as against the S&P 500 using the SPY ETF proxy from February 2006 to-date.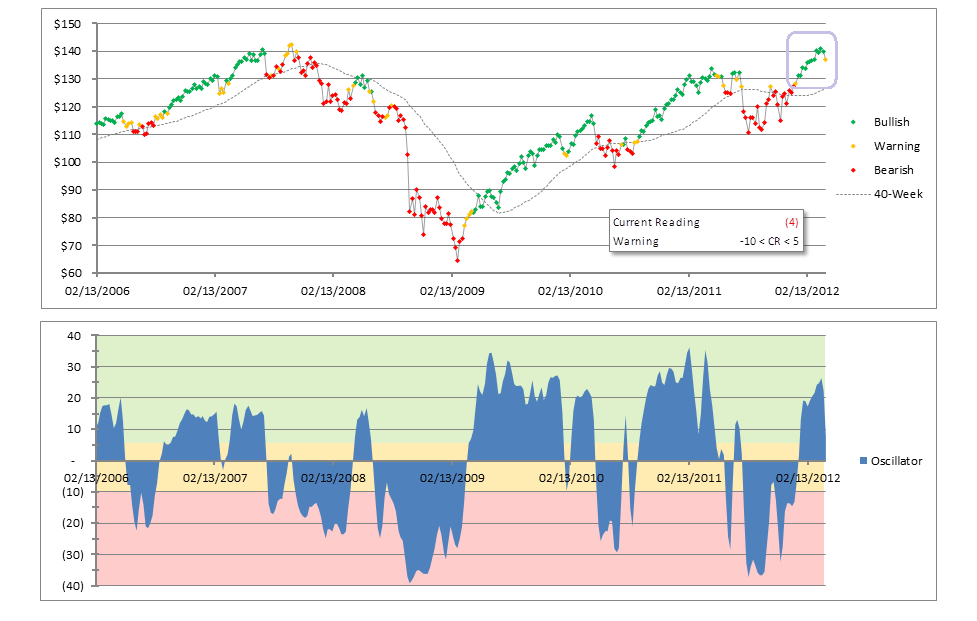

The oscillator maybe constructed using a variety of approaches, including slope scoring, relative price versus moving average positioning, and others, then summing all those ordinalized scores across the selected ETFs and setting oscillator bounds. Really, the possibilities are endless — experiment away!

Now, most of my other models are still seeing “Risk On”, even if at a moderated level, so this is really just an early heads-up. More often than not the warnings are false positives, but it’s also true that they nearly always precede full volatility events. For the bull’s sake, let’s therefore hope it’s not a canary in the coal mine this go around.

Degrees of Confidence

The way I use these types of models is as warnings to consider hedging or exposure management. What I especially like about this type of modeling approach, is that it features diverse securities over single proxies, and is multi-state rather than simply binary. In my mind this affords such models a higher degree of confidence and nuance in their output over and above more level-one type approaches, such as single period moving averages against any single given underlying.