Something interesting has been happening in gold over the last decade.
I know that sounds strange, but what has been happening is interesting in a very specific way: gold has been outperforming a priori expectations for returns, by a significant margin. So far, that’s still not very interesting since just about every asset class has been outperforming a priori expectations for returns for quite a while.
That’s what excess liquidity provision will do (and is supposed to do), after all. But what’s interesting about gold is that for a very long time the relationship between the starting real price of gold and the subsequent real return has been very strong, and it still is—but the relationship seems to have shifted.
Naturally, the key to good long-term returns is buying at low prices and selling at high prices. But the question of what “high” and “low” prices are is the squishy part. In gold, though, it turns out that going back for quite a while the subsequent real return to gold has been strikingly regular.
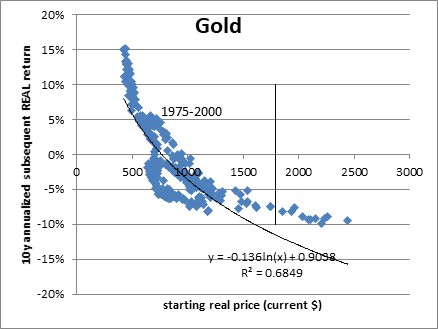
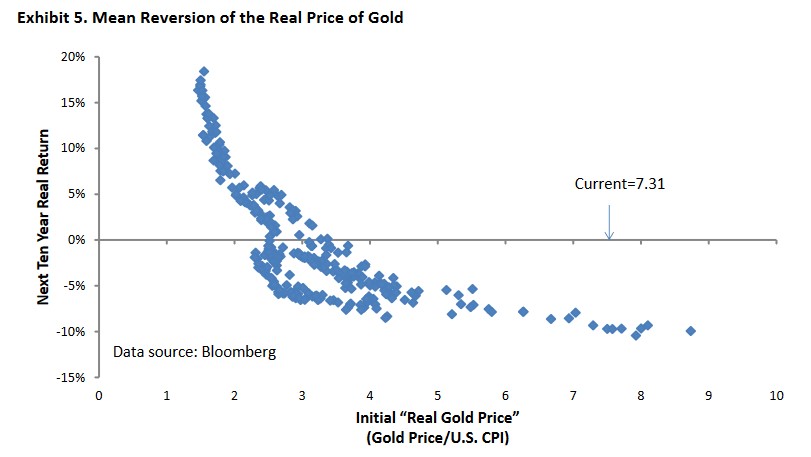
The chart below is snipped from Erb and Harvey’s “The Golden Dilemma,” an excellent paper published in 2013. It shows the subsequent 10-year annualized after-inflation return to gold, as a function of its starting real price (defined by E&H here as simply the gold price divided by the CPI Index).
The chart below shows this relationship as I’ve recreated it, but putting the prices relative to the current spot price (that is, adjusting past prices by the ratio of the current CPI price level index to the CPI Index at that time). This is for periods starting 1975-2000 and ending therefore 1985-2010.
Unsurprisingly, it matches Erb & Harvey except for the different ending point, and the choice of how the x-axis is represented. I’ve also drawn a log regression line here. Obviously there should be a bit more curvature to the line but you get the idea.
It’s a pretty decent fit: tell me the starting price in today’s dollars and I can give you a pretty accurate guess at the future real return. Lower prices lead to better subsequent real returns. The current price, though (where the vertical line is drawn), is not encouraging.
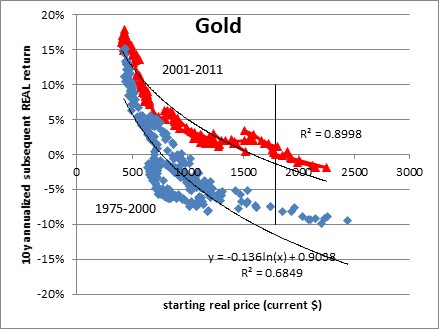
But here’s where the interesting part comes in. The next 10 years’ worth of starting points and ending points, after those plotted above, still fall on a very nice curve. But the curve is a lot higher.
This is much more encouraging! Whereas the original curve suggested that the expected real return to gold, starting from the current price, is presently about -8% per annum, the more recent curve suggests that the expectation should be roughly a 0% real return.
That is, gold ought to approximately keep up with the price level. The curve in red is also more encouraging in that it suggests that while you can have great real returns by buying gold when it occasionally gets quite cheap, it shouldn’t drastically underperform inflation even when it gets kinda expensive. That’s great news for owners of gold, if we can believe it.
I have one mild concern, though—what caused this shift in curves? Clearly, gold has done wonderfully since 2001 partly because it started at a very low real price but also partly because the tremendous liquidity that has been a feature of the financial landscape for the last 13 years (at least) has raised all “real” boats.
Because it turns out that gold—more so than a lot of other commodities—also reacts fairly directly to real interest rates. In a study that we did as part of our work with Simplify Asset Management, we found that for one-year horizons, gold has approximately 4 times as much duration with respect to real interest rates than it does to the price level, and the delta to the 10-year real interest rate is about 10x. That is, if real interest rates drop 1%, then that effect alone will influence gold to rise about 10%.
Thus, at least some of what is happening here is that the ‘new curve’ reflects the steady decline in 10-year real interest rates since the late 1990s, from a bit above 4% to the neighborhood of -1% now. Given the (current) starting real price of gold, our expectation for gold’s return over the next decade is that it should be roughly equal to the aggregate inflation over that time frame.
The caveat, though, is significant. If real interest rates rise during that time, then gold will probably underperform inflation. Only if real interest rates fall appreciably further—which seems unlikely—can we concoct a scenario where we would think a priori that gold should beat inflation comfortably.
And that means that even if you think the red dots in the plot above are a better basis for a forecast, the net message should still not be overly bullish for gold. The most optimistic guess would be that gold’s return equals the change in CPI, unless interest rates collapse further.
However, that circumstance is not damning to gold alone; just about every asset class is subject to the same law of liquidity/gravity. Take away liquidity, and real interest rates tend to rise. Take away liquidity, and prices of all sorts of assets decline, to some level where they’ll offer a better future return from a lower starting price.