In my last post, “You Have Not Missed It,” I promised the following:
“There is one final point that I will explain in more detail in another post. Breakevens also should embed some premium because the tails to inflation are to the upside. When you estimate the value of that tail, it’s actually fairly large.”
So, as promised, here is that explanation.
Viewing the forward inflation curve as a forecast of expected inflation (whether using “breakevens” or, more accurately, inflation swaps) is biased in a particular way. Or, at least, it should be.
The “breakeven” inflation rate is the rate at which a long-only investor over the ensuing period would be roughly as well off with a nominal bond (which pays a real rate plus a premium for expected inflation) and an inflation-indexed bond (which pays a real rate, plus actual inflation realized over the period).
Obviously the inflation-indexed bond is safer in real space, so arguably nominal bonds should also offer a risk premium to induce a buyer to take inflation risk.[1] Ordinarily, though, we ignore this risk and just consider breakeven inflation to be the difference between real and nominal yields.
Inflation swaps are cleaner, in that if inflation is higher than the stated fixed rate, the fixed-rate payer on the swap ‘wins’ and receives a cash flow at the end, whereas if inflation turns out to be lower than the stated fixed rate, it is the fixed-rate receiver who wins.
So from here on, I will talk in terms of inflation swaps, which also abstract from various bond-financing issues of the breakeven…but the reader should understand that the concept applies to other measures of expected inflation as well.
Now, suppose that you expect 10-year inflation to come in at 2% per annum. Suppose that in the inflation swap market, the 10-year rate is 2% ‘choice’—that is, you may either buy inflation at 2% or sell inflation at 2%. Since you expect inflation to be 2%, are you indifferent about whether you should buy or sell?
The answer is no. In this case you should be much more eager to buy 2% than to sell 2%, given that your point estimate is 2%. The reason why is that the distribution of inflation outcomes is not symmetrical: you are much more likely to observe a miss far above your expectation than to observe a miss far below your expectation.
Therefore, the expected value of that miss is in your favor if you buy the inflation swap (pay fixed and receive inflation) at 2%. There is, in other words, an embedded option here that means the swap market should trade above where most people expect inflation to be.
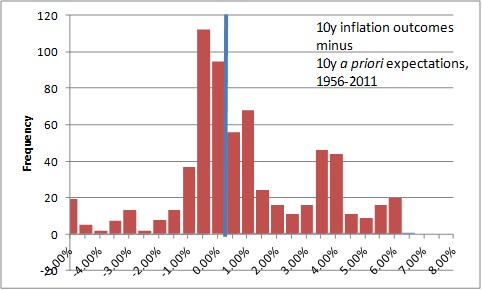
We can roughly quantify at least the order of magnitude of this effect. Consider the distribution below.
This chart shows the difference, from 1956 until 2011, of 10-year inflation expectations[2] compared with subsequent 10-year actual inflation results. The blue line is at 0%—at that point, actual inflation turned out to be right where a priori expectations had it. The chart obviously only covers until 2011 since that is the last year from which we have a completed 10-year period. Recognize that I am not charting the levels of inflation, but the level of inflation relative to the original expectation.
Notice that the chart has a cluster of outcomes (and in fact, the most-probable outcomes) just to the left of zero, where expectations exceeded the actual outcome by a little bit, but that there are very few long tails to the left. However, misses to the right, where the actual outcome was above the beginning-of-period expectations, were sometimes quite large.
The median point (where half of the misses are to the left, and half are to the right) is 0.21%. But this is not a symmetric distribution, so if we randomly sample points from this distribution, we find that the average of that sample is 0.59%.
So, if you buy the inflation swap at 2% when your expectations are at 2%, on average you’ll win by 59bps, at least historically. Of course, past results are no indication of future returns, and a Fed economist would argue that we have much better control of inflation now than we ever have in the past (Ha ha. I crack myself up.).
And inflation volatility markets, when they can be found, don’t trade at such high implied volatilities. Noted, although the wild swings in growth and the deficit and the money supply, not to mention recent realized outcomes, might make more cynical observers question whether we should be so confident in that view right at the moment.
Moreover, a counterargument is that at the present time, an investor also has the advantage of investing when expectations are fairly low, so the downside tails are not as likely.
The worst outcome of that whole 1956-2011 period was an 8.75% undershoot of inflation versus expectations. This happened in the 10 years following September 1981, when expectations were for 10-year inflation of 12.70% and actual inflation was 3.95%.
But with expectations at 2.50%, is it really feasible to get a -6.25% compounded inflation rate? That would imply a 50% fall in the price level (and, I should note, it would mean that investors in TIPS would win hugely in real space since they get back no worse than nominal par. But that doesn’t help the swap buyer).
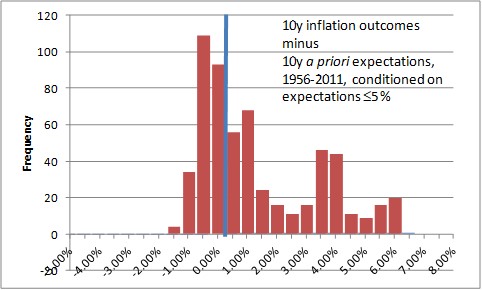
To be a little more fair, then, the following chart considers only the periods where inflation expectations were 5% per annum or less at the beginning of the period. That truncates only 10% of the distribution, but as you might expect the vast majority of the truncation is on the left-hand side. This is fair because it’s naturally harder to miss far below your expectations when your expectations are very low to begin with.[3]
The value of the expected miss in this contingent view is 1.13%. So, in order for the market to be priced fairly if general expectations are for 2.5% average CPI inflation, the 10-year inflation swap would have to be around 3.63%. Again, even allowing for the “policymakers are smarter now” argument (an argument quite lacking, I would argue, in empirical evidence) I would feel comfortable saying that 10-year inflation swaps, and breakevens, should embed at least a 50bps or so ‘option premium’ relative to expectations.
I don’t believe that they do. Indeed, consider that the buyer of 10-year TIPS (with breakevens at 2.50%) not only wins if 10-year inflation is above 2.50%, but the average win historically (conditioned on breakevens being below 5% to start, and by construction only considering wins) has been about 2.07% per annum—a massive outperformance.
Not only that, but any losses are essentially guaranteed to be small because the tails on the left-hand side are truncated: if inflation is negative (that is, if the loss would have been greater than 2.50%) it is limited by the fact that the Treasury guarantees the nominal principal.
As an aside, we do consider this sort of option in other contexts. In the Eurodollar futures market, for example, we recognize that the person who is short the Eurodollar contract (and therefore gets a positive mark-to-market when interest rates rise) is in a better situation than the long (who gets the positive mark-to-market when interest rates fall), because the short gets to invest wins at higher interest rates and borrow losses at lower interest rates, while the long must borrow to cover losses when interest rates are higher, and gets to invest wins when interest rates are lower.
As a result, Eurodollar futures trade lower than the forwards implied from the swap curve, since the buyer needs to be induced by a better-than-expected price. And there are other such examples. But I am pretty sure I have never seen an example of an embedded option like this that is priced so differently relative to history than the embedded options in the inflation market!
[1] However, since this risk is symmetric—the seller of the bond also has risk in real space, but in the opposite direction—it isn’t immediately obvious why one side should get an inducement over the other. So I will leave the ‘risk premium’ aside.
[2] For long-term inflation expectations back before the advent of TIPS, I used the Enduring model relating real yields to nominal yields, about which I’ve written previously. You can find a brief discussion of this and an illustration of the model in this past article.
[3] The author’s wife has been known to make this type of observation from time-to-time.