It has been a long time since we have had to worry about and think about the phenomenon of mortgage convexity and the effect that it can have on the bond market. But with 10-year interest rates up 50bps in less than 1 month, and some of the selloff recently being attributed to “convexity-related selling,” it is worth reminiscing.
We need to start with the concept of “negative convexity.” This is a fancy way of saying that a market position gets shorter (or less long) when the market is going up, and longer (or less short) when the market is going down. That’s obviously a bad thing: you would prefer to be longer when the market is going up and less long when the market is going down (and, not surprisingly, we call that positive convexity).
Now, a portfolio of current-coupon residential mortgages in the US exhibits the property of negative convexity because the homeowner has the right to pre-pay the mortgage at any time, and for any reason – for example, because the home is being sold, or because the homeowner wants to refinance at a lower rate. Indeed, holders of mortgage-backed securities expect that in any collection of mortgages, a certain number of them will pre-pay for non-economic reasons (such as the house being sold) and the rest will be pre-paid when economic circumstances permit.
Suppose that in a pool of mortgages, the average mortgage is expected to be paid off in (just to make up a number, not intended to be an accurate or current figure) ten years. This means that the security backed by those mortgages (MBS for short) would have a duration of about ten years, so that a 1% decline in interest rates would, in the absence of convexity, cause prices to rise about 10%.[1]
Now, that’s really just a guess based on where interest rates are currently. As interest rates change, so does the duration of the bond. If mortgage interest rates fall significantly, then most of the mortgages in that MBS would pre-pay and the duration of the security would fall sharply.
Suppose that after a sufficient decline in interest rates, the same pool of mortgages in that MBS is expected to be pre-paid on average in only 3 years. Now a further 1% rise in interest rates will only cause the price of the MBS to rise about 3%. This is negative convexity, and what is significant here is how holders of MBS respond. In order to maintain a similar market exposure, the owner of the MBS needs to buy more bonds, swaps, or MBS to maintain his duration. That is, into a rally, the MBS owner needs to buy more. This is “buying high,” and it’s the manifestation of one side of that negative convexity.
Suppose that instead, interest rates rise sharply. Now, instead of expecting those mortgages to economically pre-pay over the next 10 years, we realize that the opportunities for these homeowners to refinance just went away (at least for a while); consequently, we now expect the mortgages to pay off in 15 years on average, rather than 10. A further rise of 1% in interest rates will cause prices to fall 15% rather than 10%. Again, the MBS holders need to respond, and they do so by selling bonds, swaps, or MBS to maintain duration. That is, into a selloff, the MBS owner needs to sell more. This is “selling low,” and it’s the manifestation of the other side of that negative convexity.
Put together, a manager of a large MBS portfolio is earning a higher-than-average coupon, but is also systematically buying high and selling low on his hedges and losing a little money each time. More importantly for our case here is that if the market moves enough to trigger the hedging activity then we say that “the convexity trade” has caused a significant amount of selling into a selloff, or a significant amount of buying into a rally, and this essentially means fuel is being added to the fire and the move is worsened. The mortgage market is massive, and especially with dealers having less capacity for market-making risk-taking a big convexity trade could cause a huge move. In the 2000s, I recall two massive selloffs of at least 125bps over a period of just a few weeks, in which every 5bps seemed to bring out another huge seller and push the market another 5bps.
Figuring out exactly what the trigger level is at which the convexity trade kicks in is the domain of mortgage analysts, and there is a lot of brainpower and computing power put to this analysis. These folks can tell you that “a 10-year note rate of 2.25% will cause the market to get longer by 150bln 10-year note equivalents [just to be clear, this is a made up example],” which in turn implies that there will be substantially more selling when interest rates approach that level.
Now, I don’t know what the current trigger levels are, but I can tell you a few more things from years of experience.
First is that the market’s negative convexity is greatest when the market has rallied to a new level and stayed there for a long time, allowing most borrowers to refinance their mortgages to the current coupon. The chart of 10-year yields below (Source: Bloomberg) illustrates this point. In 2008, 10-year note yields fell below 2.5%, but did so very quickly and few people had a chance to refinance (plus, mortgage spreads were quite wide and credit was hard to get), so the mortgage market maintained something like its prior equilibrium.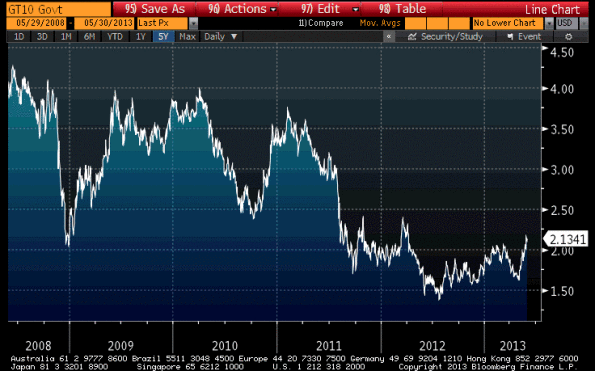
However, over 2010 and especially after mid-2011, rates got substantially lower and stayed lower; mortgage credit also got somewhat easier than in early 2009 (although obviously underwater homeowners cannot refinance, and this limited the amount of refinancing activity so that MBS prepay speeds weren’t as rapid as the pre-2008 models had expected). We have now been at these levels for some time, so that I suspect the market’s average coupon is substantially lower today than it was two years ago. This means the bond market is very vulnerable to a convexity trade to higher yields, especially once the ball gets rolling. The recent move to new high yields for the last 12 months could trigger such a phenomenon. If it does, then we will see 10-year note rates above 3% in fairly short order.
The second point is somewhat more subtle. The nature of the negative convexity in the higher rate direction is different from the nature of the negative convexity in the lower rate direction. When rates fall, we are looking at borrowers refinancing, which means that we can stair-step lower: rates fall, borrowers refinance, rates fall further, borrowers refinance again, etcetera. But when rates rise, the duration increase is caused by a lack of activity. Borrowers eschew refinancing. And this, fundamentally, can only happen once no matter how far rates move. If it is not economical to refinance with rates 2% higher, then few borrowers will refinance. But at 5% higher rates, there is no additional effect: once your model expects essentially zero refinancing, the convexity trade is over until you get substantial new origination of mortgages, and this takes longer. Therefore, in a selloff the convexity trade is somewhat self-limiting. It sure doesn’t feel like it at the time, but it is.
This is a long article but it is worth reflecting on because of the conclusion, and that is this: if rates rise because the Fed begins to raise rates (or finds it doesn’t have enough will to keep them low, once the bond market expects much higher inflation), then there is no “cap” on how high they can go. But if rates rise in a sloppy fashion because of a convexity trade, there really is a cap. It would be ugly to see interest rates rise another 100bps (and really, really bad for stocks I think), but if they did so because of the convexity trade then we would probably get a bunch of that move reversed thereafter.
I don’t have a strong opinion about whether we are at that point yet, and I no longer have access to great mortgage analysts. But Fed speakers should tread very lightly, as I doubt the first trigger point is terribly far away and you surely don’t want to hit it.
There is one reason I don’t think that the bond market selloff we have seen to date is heavily driven by convexity-related flows, and that is that TIPS yields have risen faster than nominal bond yields. Over the period during which nominal 10-year yields have risen 50bps, 10-year TIPS yields have actually risen 58bps. If the trade was a convexity-driven trade, it would be primarily affecting nominal yields, which means that while TIPS would be suffering, they would be suffering less than nominal bonds, rather than more. (The flip side is that if you are bearish here because you think the convexity trade might kick in, you should also expect breakevens to widen substantially when that trade does kick in). Indeed, TIPS at -0.13% is the best bargain we have seen in quite some time (see chart, source Bloomberg). 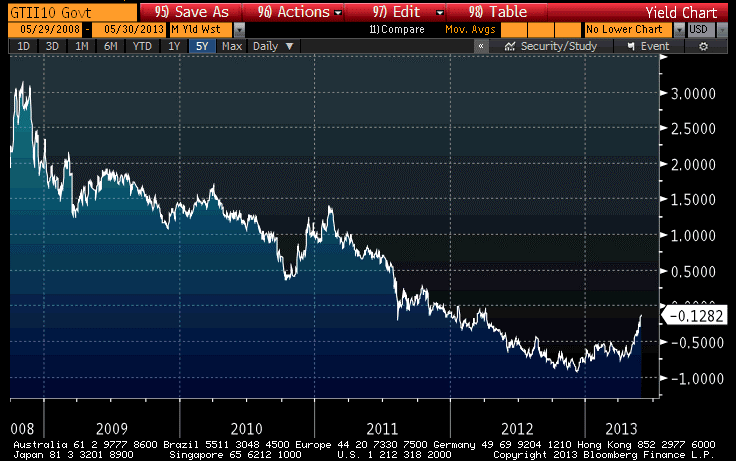
Indeed, our multi-asset strategy has kicked the TIPS component all the way up to 11%, which is the highest it has been in a long while. TIPS are not cheap, but they are cheaper, and they are extremely cheap relative to nominal bonds. And they are not yet as cheap as i-Series savings bonds, although the yield advantage of those bonds has dropped from the 159bps it was when I wrote about it here to “only” 93bps. But that’s still a great arb, and so I continue to advocate i-bonds.
[1] I am abstracting from the niceties of Macaulay versus modified versus option-adjusted duration here for the purposes of exposition.
- English (UK)
- English (India)
- English (Canada)
- English (Australia)
- English (South Africa)
- English (Philippines)
- English (Nigeria)
- Deutsch
- Español (España)
- Español (México)
- Français
- Italiano
- Nederlands
- Polski
- Português (Portugal)
- Português (Brasil)
- Русский
- Türkçe
- العربية
- Ελληνικά
- Svenska
- Suomi
- עברית
- 日本語
- 한국어
- 简体中文
- 繁體中文
- Bahasa Indonesia
- Bahasa Melayu
- ไทย
- Tiếng Việt
- हिंदी
Bonds And The 'Convexity Trade'
Latest comments
Loading next article…
Install Our App
Risk Disclosure: Trading in financial instruments and/or cryptocurrencies involves high risks including the risk of losing some, or all, of your investment amount, and may not be suitable for all investors. Prices of cryptocurrencies are extremely volatile and may be affected by external factors such as financial, regulatory or political events. Trading on margin increases the financial risks.
Before deciding to trade in financial instrument or cryptocurrencies you should be fully informed of the risks and costs associated with trading the financial markets, carefully consider your investment objectives, level of experience, and risk appetite, and seek professional advice where needed.
Fusion Media would like to remind you that the data contained in this website is not necessarily real-time nor accurate. The data and prices on the website are not necessarily provided by any market or exchange, but may be provided by market makers, and so prices may not be accurate and may differ from the actual price at any given market, meaning prices are indicative and not appropriate for trading purposes. Fusion Media and any provider of the data contained in this website will not accept liability for any loss or damage as a result of your trading, or your reliance on the information contained within this website.
It is prohibited to use, store, reproduce, display, modify, transmit or distribute the data contained in this website without the explicit prior written permission of Fusion Media and/or the data provider. All intellectual property rights are reserved by the providers and/or the exchange providing the data contained in this website.
Fusion Media may be compensated by the advertisers that appear on the website, based on your interaction with the advertisements or advertisers.
Before deciding to trade in financial instrument or cryptocurrencies you should be fully informed of the risks and costs associated with trading the financial markets, carefully consider your investment objectives, level of experience, and risk appetite, and seek professional advice where needed.
Fusion Media would like to remind you that the data contained in this website is not necessarily real-time nor accurate. The data and prices on the website are not necessarily provided by any market or exchange, but may be provided by market makers, and so prices may not be accurate and may differ from the actual price at any given market, meaning prices are indicative and not appropriate for trading purposes. Fusion Media and any provider of the data contained in this website will not accept liability for any loss or damage as a result of your trading, or your reliance on the information contained within this website.
It is prohibited to use, store, reproduce, display, modify, transmit or distribute the data contained in this website without the explicit prior written permission of Fusion Media and/or the data provider. All intellectual property rights are reserved by the providers and/or the exchange providing the data contained in this website.
Fusion Media may be compensated by the advertisers that appear on the website, based on your interaction with the advertisements or advertisers.
© 2007-2025 - Fusion Media Limited. All Rights Reserved.
